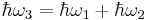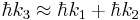Sum-frequency generation
Sum-frequency generation (SFG) is a non-linear optical process. This phenomenon is based on the annihilation of two input photons at angular frequencies 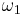 and
and 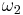 while, simultaneously, one photon at frequency
while, simultaneously, one photon at frequency 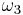 is generated. As with any phenomenon in nonlinear optics, this can only occur under conditions where:
is generated. As with any phenomenon in nonlinear optics, this can only occur under conditions where:
- The light is interacting with matter;
- The light has a very high intensity (typically from a pulsed laser).
Sum-frequency generation is a "parametric process",[1] meaning that the photons satisfy energy conservation, leaving the matter unchanged:
A special case of sum-frequency generation is second-harmonic generation, in which ω1=ω2=½ω3. In fact, in experimental physics, this is the most common type of sum-frequency generation. This is because in second-harmonic generation, only one input light beam is required, but if ω1≠ω2, 2 simultaneous beams are required, which can be more difficult to arrange. In practice, the term "sum-frequency generation" usually refers to the less common case where ω1≠ω2.
For sum-frequency generation to occur efficiently, a condition called phase-matching must be satisfied:[2]
where 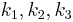 are the angular wavenumbers of the three waves as they travel through the medium. (Note that the equation resembles the equation for conservation of momentum.) As this condition is satisfied more and more accurately, the sum-frequency generation becomes more and more efficient. Also, as sum-frequency generation occurs over a longer and longer length, the phase-matching must become more and more accurate.
are the angular wavenumbers of the three waves as they travel through the medium. (Note that the equation resembles the equation for conservation of momentum.) As this condition is satisfied more and more accurately, the sum-frequency generation becomes more and more efficient. Also, as sum-frequency generation occurs over a longer and longer length, the phase-matching must become more and more accurate.
Some common SFG applications are described in the article sum frequency generation spectroscopy.